Points de fuite.

Bon, par quel bout commencer?

Peut être tout simplement en remarquant que deux droites parallèles (des rails de chemin de fer par exemple) mais non perpendiculaires à la direction du regard semblent se rejoindre en un point. Si ces droites appartiennent à un plan horizontal (tel que le sol), elles sembleront fuir vers un point situé sur l'horizon.

D'ailleurs, il serait plus juste de dire que l'horizon est constitué de l'ensemble des points de fuite des faisceaux de droites parallèles appartenant à des plans horizontaux.

De même, l'ensemble des plans verticaux parallèles à la direction de regard a un seul et même horizon (lui-même constitué de l'ensemble des points de fuite des droites comprises dans ces plans verticaux) : l'axe vertical de la fenêtre de visée.

A la jonction de ces deux horizons (le vertical et l'horizontal) se trouve un point particulier. C'est le point de fuite de toutes les droites parallèles à la direction du regard.

Pour leur part, des droites parallèles entre elles perpendiculairement à la direction du regard ont une particularité fort utile et intéressante : elles sont perçues par l'oeil comme des lignes équidistantes (représentées par des parallèles donc).

Arrivée là, je me rend compte qu'il peut être bon de préciser quelque chose qui va sans dire, mais qui va mieux en le disant. En faisant de la perspective, on représente un espace à 3 dimensions sur un espace qui n'en a que 2. Il faut donc toujours faire nettement la distinction entre l'objet et l'image qu'on en fait.
Dans l'espace, deux droites parallèles restent toujours séparées par la même distance et n'ont donc aucun point commun (ou alors elles sont confondues ^^ ) alors que sur la feuille on les restitue par deux demi-droites partageant la même origine et formant un angle dont la valeur dépend de la position des droites observées par rapport à l'observateur. De même, la mesure d'un angle droit dans l'espace sera toujours de 90° alors que sur la feuille, la mesure apparente de ce même angle sera comprise entre 0° et 180°.

Ces constats et cette digression faits, voyons quel usage on peut en avoir.

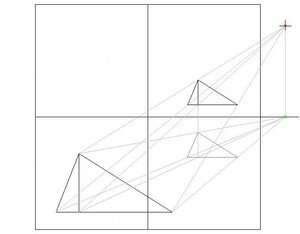
On voit que toutes les droites émergeant d'un même point de fuite seront parallèles entre elles, ce qui fait que si on relie les sommets d'une figure en position frontale (perpendiculaire à la direction du regard) à un point de fuite, on pourra la déplacer le long de ces lignes de fuite comme sur des rails. Si on utilise le point de fuite central, on sait aussi par avance que les lignes de fuite seront perpendiculaire au plan frontal. Le fait que la figure initiale soit en position frontale permet de tracer les cotés de la figure finale en tirant simplement les parallèles aux cotés de la première.

Ça peut sembler trivial, mais ça permet déjà de construire toute sorte de chose ayant des cotés parallèles ou perpendiculaires ou les deux. Par contre, ça ne suffit pas à construire un cube puisqu'avec ce dont on dispose, on ne peut pas comparer les longueurs des lignes fuyantes et des lignes frontales.

Prochaine étape : les points de fuite diagonaux ou comment établir une relation entre des distances frontales et fuyantes.